Tianhao's Blog
0%

Posted on

占用率 (Occupancy)

占用率表示GPU正在运行的线程块和理论上能运行的最大线程块数量的比值。它可以反映GPU在给定时间点上背有效利用的程度。GPU占用率公式： \[ Occupancy = \frac{Active \ warps}{Max \ warps\ per \ SM} \] GPU的占用率被每一个thread block使用的资源量制约。制约的资源包括：寄存器数量，共享内存，Block 大小，和其支持最大并发线程数，分支与同步。

  • 寄存器数量限制：

    假设设备的 registers / SM 是 32k，最大支持 1536 threads / SM - 即最大支持48个warp。

    若每个 thread 用63个寄存器，那么 32k / 64 = 512 threads。Occupancy: 512 / 15366 =0.0333

    threadPerBlock.jpg

    当register / thread 增大，occupancy阶梯式会下降。阶梯式是因为SM是以warp为单位执行的。当register多到需要去除掉一个active warp时才会下降。

  • 共享内存限制：

    假设设备的 shared memory 是 48kb

    若每个 thread 使用 64b 的共享内存，那么一共支持 48k / 64 =768 个线程。Occupancy: 768 / 1536 = 0.5

  • Block size 限制：

    假如设备每个SM最多能放8个block，如果block小，那么SM就无法包含足够的warp。

    blocksize.jpg

    一开始时递增是因为block太小，warp不够多。在 \(block = 128\) 时warp达到最大，然后进入波动。波动的原因也是因为block size 内剩余的thread不足以构成一个warp。不同block的thread又无法组成新warp，因此会浪费掉一些占用率。

优化思路：

高占有率并不代表高性能，根据 Vasily Volkov 的研究，达到期待性能所需要的GPU性能所需占用率与计算强度有关。

Vasily Volkov.jpg

  • 当计算强度低时，内存延迟成为主要瓶颈，需要更高的GPU占用率来隐藏延迟。（有更多的warp来切换）

  • 当计算强度高时，GPU计算单元充分利用，不需要频繁切换warp，需要考虑优化指令效率等

低占用率过低可能是优化机会，可以调大线程块大小，减少单线程对寄存器和共享内存的使用。

Little's Law in GPU

在GPU中我们也可以算出想要保持硬件满负载，SM要同时处理多少个warp的指令。例如：kepler有192个核心，1个warp执行一个指令要做32个操作。

  • 那么每个cycle，SM可以同时处理 \(192 / 32 = 6\) 个warps。假设每个instruction有9个cycle的延迟，那么想要保持硬件满负载我们需要 \(9 \times 6 = 54\) 个warps。

这里我们也可以计算出内存操作需要多少并发度来隐藏延迟。若有一个机器，访问内存的延迟为 386 cycles，一共16个SM，每一次load会合并128B的数据传回，带宽为211GB/sec，机器的频率时1.266GHz。

  • 那么每个cycle，可以从内存里传输来的数据为 \(211 / 1.266 =166.67B\) 。由于每次load instruction可以传回\(128B\)的数据，那么设备的吞吐量为 \(166.67 / 128 = 1.30 \text{ instructions per cycle}\)。由于我们有16个SM，每一个SM的吞吐量为 \(1.3 / 16 = 0.081\)。那么我们每一个SM需要的并行指令数为 \(386\times 0.081 = 32 \ (取整)\)，也就是说我们需要32个warps。

Thread Level Parallelism & Instruction Level Parallelism

目标：隐藏延迟 & 提高吞吐量

  • Thread Level Parallelism (TLP): 通过增加warps的数量，在等待延迟时切换到其他线程执行任务
  • Instruction Level Parallelism (ILP): 在同一个线程中发出多个相互独立的指令，在等待指令结果时运行其他指令

例如 Kepler GPU 就可以每个时钟发射两个命令。单这两个命令不能有依赖，否则将会有延迟。我们可以通过引入更多的独立指令来提高指令并行度，更好的利用GPU执行单元。

我们通常会增加TLP来追求更好的性能，然而增加TLP有一定的局限性。

  • 寄存器和共享内存这种硬件资源限制了TLP增大
  • 当问题规模本身比较小，我们无法分配足够多线程块，导致TLP无法提高
  • 内存访问模式 (无法coaleasing) 成为瓶颈，所有的thread都在load
  • 线程之间存在依赖

TLP 和 ILP 可以互补：

  • 当TLP高，但未饱和，继续增加warp已经没有效果了，这时可以使用 ILP 来增加但线程效率，正价吞吐量。
  • 当TLP低且受到资源限制时，硬件利用率低，可以通过增加ILP来填满硬件单元，提高吞吐量。
  • 当内存延迟高，我们可以通过TLP线程切换来隐藏延迟。

Performance Prediction

prediction.jpg

总共的工作节点用时： \(W(n)\)

最长路径上的工作节点用时：\(D(n)\)

工作用时：\(T_{comp} = D(n) + \frac{W(n) - D(n)}{p}\)

p 是处理器数量

\(W(n) / D(n)\) 越大表示并行度越高

Reference

Vasily Volkov, “Understaning Latency Hiding on CPUs”, PhD Thesis, University of California, Berkeley, Summer 2016

Posted on In

GPU 存储空间架构

粗略内存架构图：

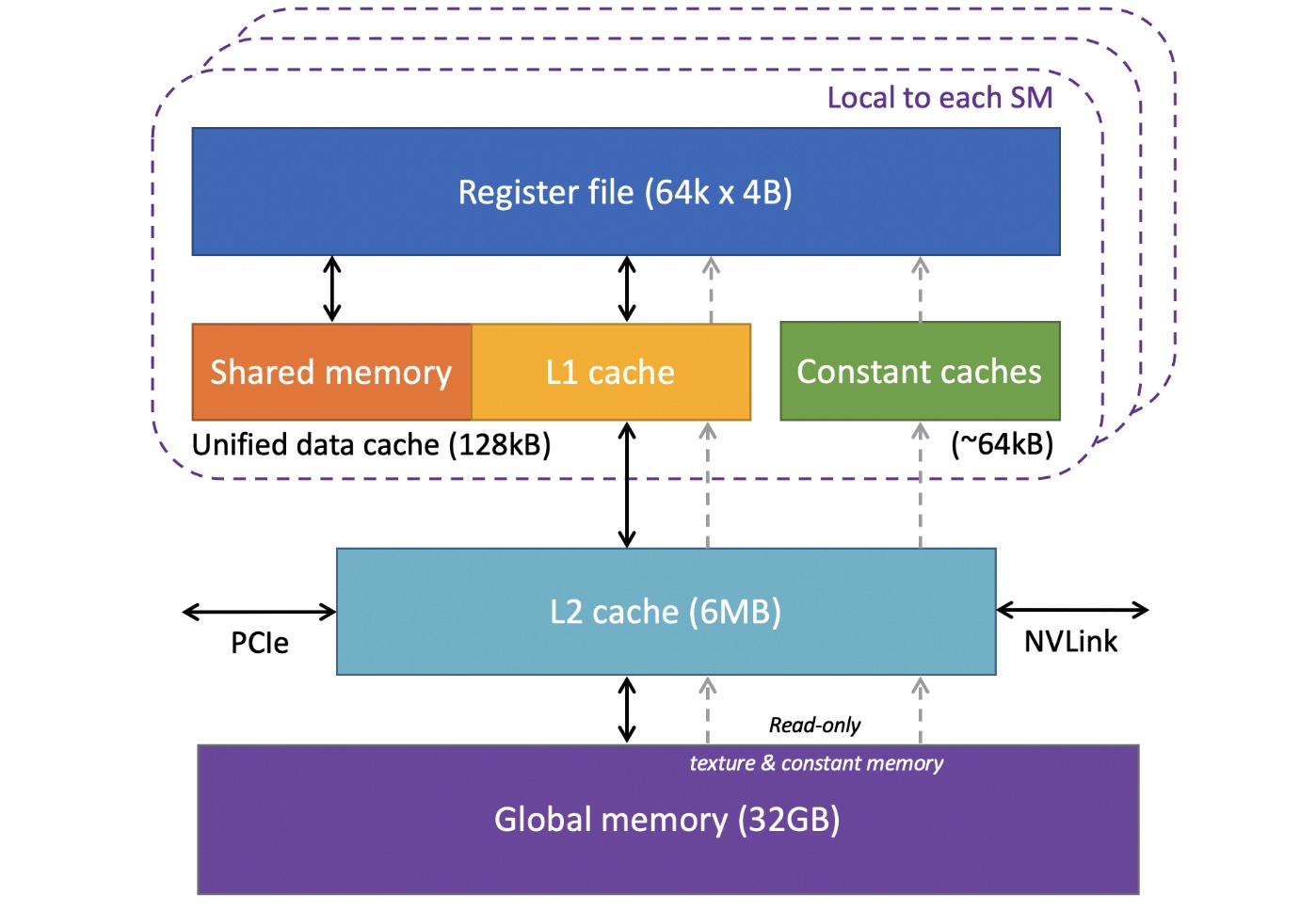
gpu_mem.jpg

内存被粗略的分为全局内存，L2缓存，L1缓存，共享内存，和寄存器文件这几层。全局内存最大但离CUDA核心最远。

缓存行被设计为 \(128 = 4 \times 32\) 个字节。由于32个id连续的线程是一个warp，一个warp执行相同的代码，因此访问操作一般是将数据传输给warp里每一个thread的。如果warp所有线程访问数据都集中在同一缓存行上，能充分利用带宽，避免浪费。

每个SM的寄存器文件被设计成"多行32列"。这是因为每个warp共有32个thread，而每个thread又使用同一个程序，也就是说在任意时间段，他们使用的寄存器都一摸一样 (即便有分枝，也知识一些线程空闲，继续其他代码操作)。因此，一个warp在执行的每个时刻会访问寄存器文件的同一行。一个程序会使用多少个寄存器会在编译时计算出来，用于warp寄存器分配。当算出需要的寄存器数量，warp会被分配多行寄存器。如果有多个warp，多个warp可以被分配到不同范围的行，从而并行执行 (可跨行分配)。当寄存器不足，会发生寄存器溢出 (register spilling)，数据会被临时存储到 L1 缓存，导致性能下降。

Shared memory 和 L1 缓存是基于bank模型设计的。Bank模型是为了让缓存的访存并行化。通常缓存被分为32个bank，与一个warp有32个thread相对应，并通过 address % bank_number 映射到对应的bank。如果一个warp内的个线程同时访存一个缓存的两个属于不同bank的数据，那么这两个线程可以并行进行访存操作。

共享内存和 L1 缓存共享物理空间，但允许线程块内的线程共享数据。常量缓存用于只读的全局变量，主要用于在warp中广播单一变量值。L2缓存是设备唯一的全局缓存，用于SM与主存之间的数据交互，同时介导设备和主机的数据传输 (使用 PCIe 或 NVlink)。

精细内存架构图：

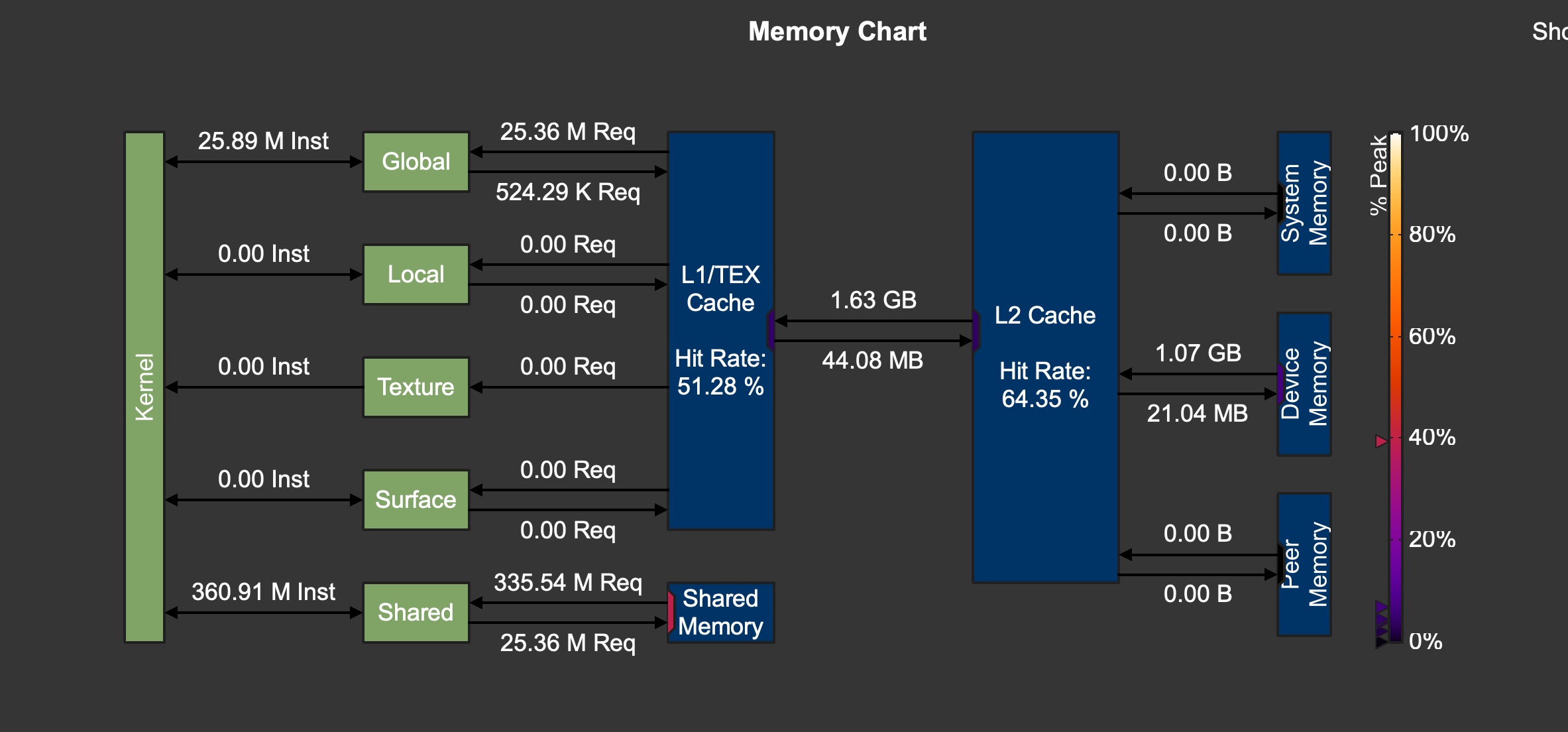
gpu-mem2.jpg

L1缓存实际被分为了：

  • Global：缓存全局内存数据，提升全局内存的读取效率
  • Local：处理寄存器溢出的本地内存数据 (局部变量)
  • Texture, Surface: 缓存纹理 & 表面数据，支持read only操作，特定图形操作

GPU之间的数据传播 & 主机到设备的数据传播都会先经过 L2 缓存，这里 L2 缓存起到了缓冲的作用，减轻了device memory的压力。

GPU 线程架构

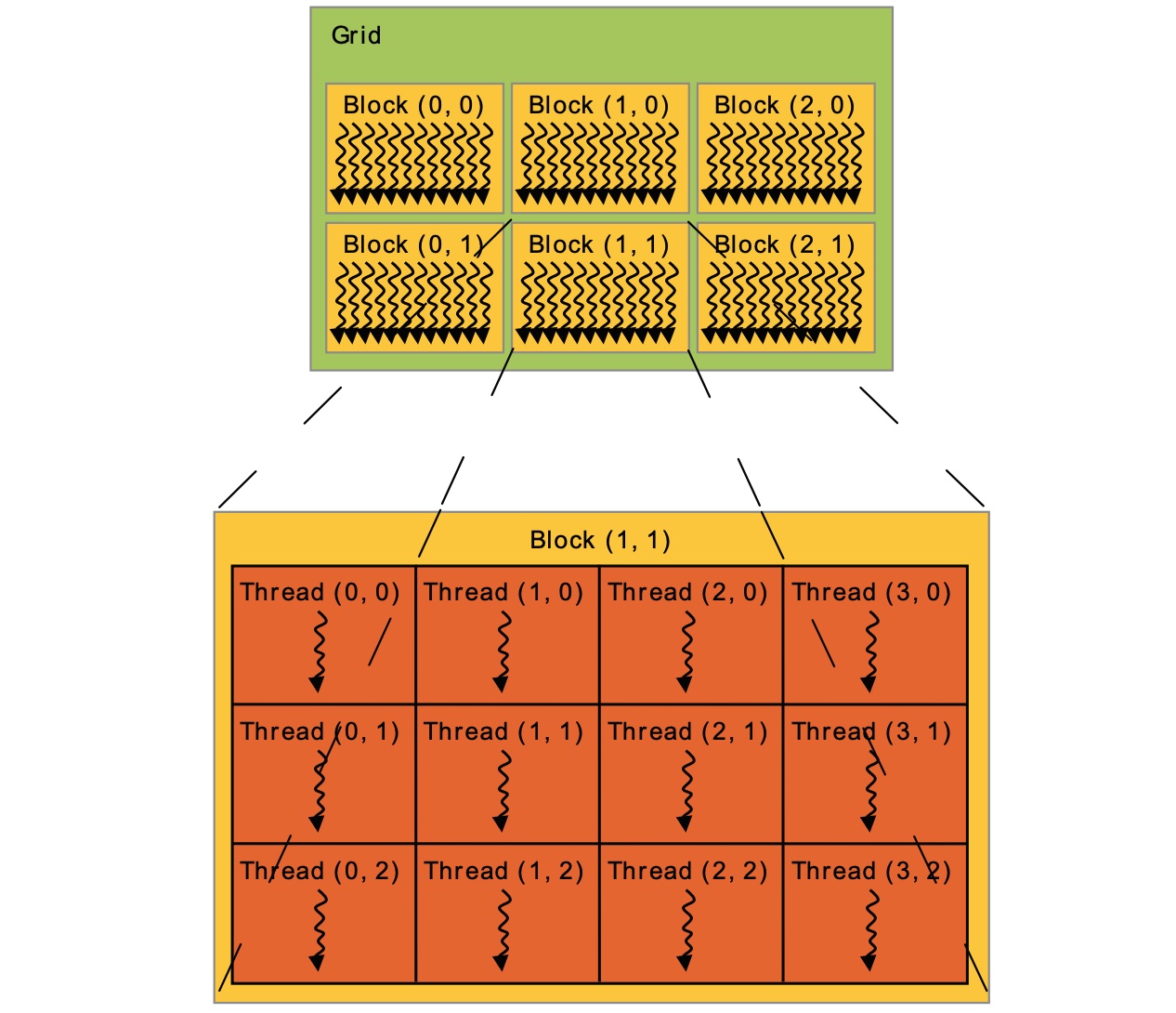
gpu_thread.jpg

在程序中，线程架构由 Grid，Block, 和 thread 构成。

计算 local thread ID :

1
threadId.x + threadId.y * blockDim.x + threadId.z * blockDim.x * blockDim.y

计算 global block ID:

1
blockId.x + blockId.y * blockDim.x + blockId.z * blockDim.x * blockDim.y

程序执行时会在启动每一个并行内核时创建一个grid (根据代码中声明的参数)

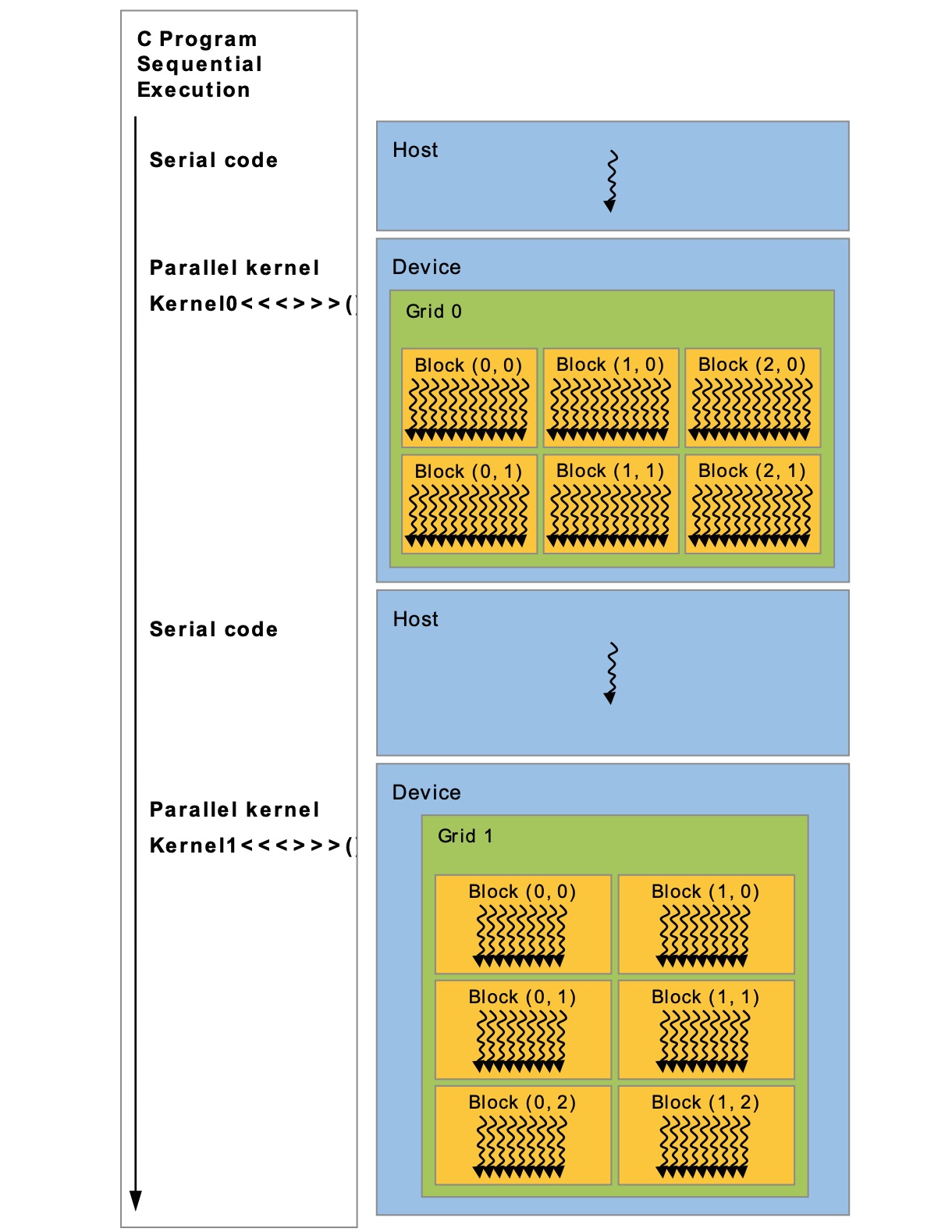
parallel_prog.jpg

一个 grid 会被提交到一个设备上，一个设备上会有多个 Streaming Multiprocessors (SMs)。grid 上的 block 会被分配到不同的 SM 中，这里会根据 SM 负载压力调度。

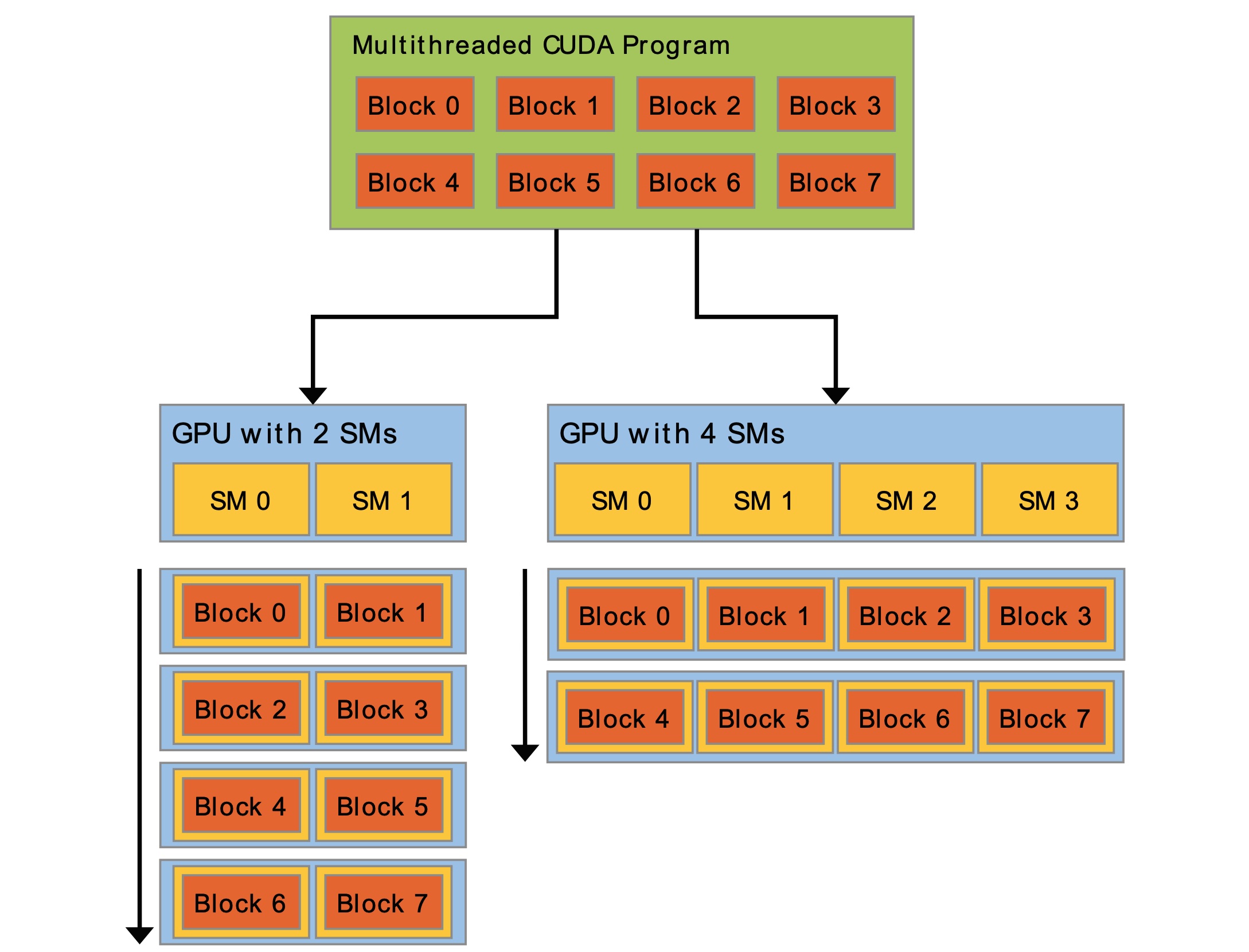
SM.jpg

硬件发展角度：Warp 及其调度

一个warp是由32个并行线程组成的线程组。这个线程组是通过划分block得来，每个warp包含连续的线程ID，从0开始划分。不同的warp间执行时独立的。在一个SM中可以存在多个warp，如果一个warp的输入操作数没有加载好，warp schedular可以切换到其他加载好的warp执行，或者是不依赖的指令执行。这里依赖编译器进行 read after write 错误，比如 fadd r4 r4 1 要用9个cycle，那么编译器不会在9个cycle调用任何使用r4的指令。

划分warp的目的时为了简化硬件设计，提高并行计算效率。Warp 时基于 SIMT (Single Instruction Multiple Threads) 架构的，结合了 SIMD 的高效性和 TLP 的灵活性。Warp 级调度可以在不同warp间无成本切换，支持高效硬件多线程。

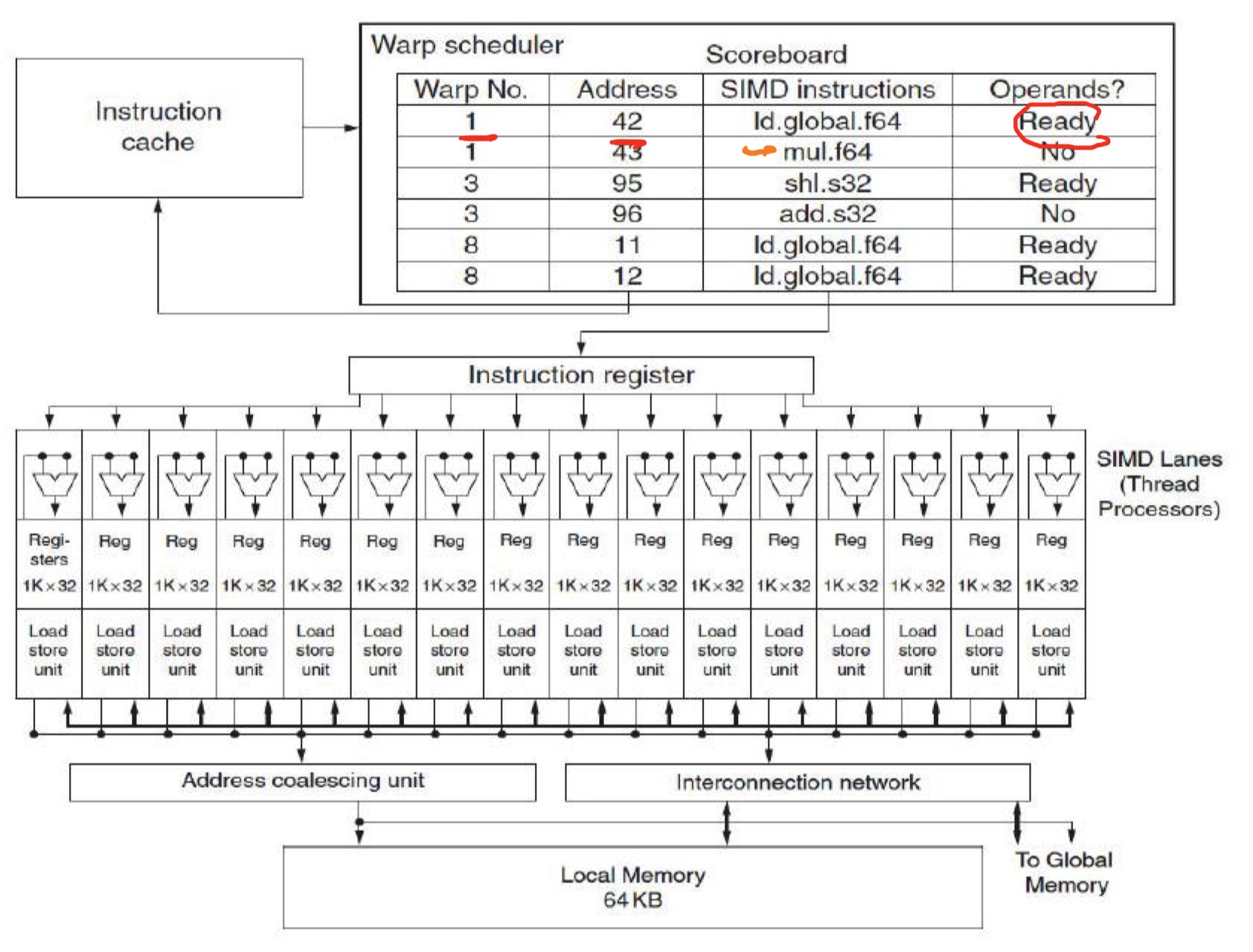
warp.jpg

Warp scheduler 维护了一个 scoreboard，用来跟踪该SM中的warp的操作数准备状态。不同block但属于同一个SM的warps 也可以调度。

  • Volta架构之前：

    我们可以假设warp内线程总是同步的，在发生分支发散时，线程会通过屏蔽非活动线程将不同的分支串行处理，简化了控制逻辑。但代价是分支发散的性能很低，我们需要尽可能避免写分支发散的代码。当然，如果分支赋予了属于不同warp的线程不同的任务是没问题的，因为只有属于一个warp的线程需要执行相同的代码。

  • Volta架构之后：

    每个线程拥有独立的程序计数器和调用栈。Warp 调度器可以在更细的粒度调度线程，不再局限于warp级别。更灵活的线程调度允许warp调度器在内存访问延迟，寄存器依赖等情况下充分利用计算资源，从而减小延迟对性能的影响。

编译：PTX 与 PTXAS

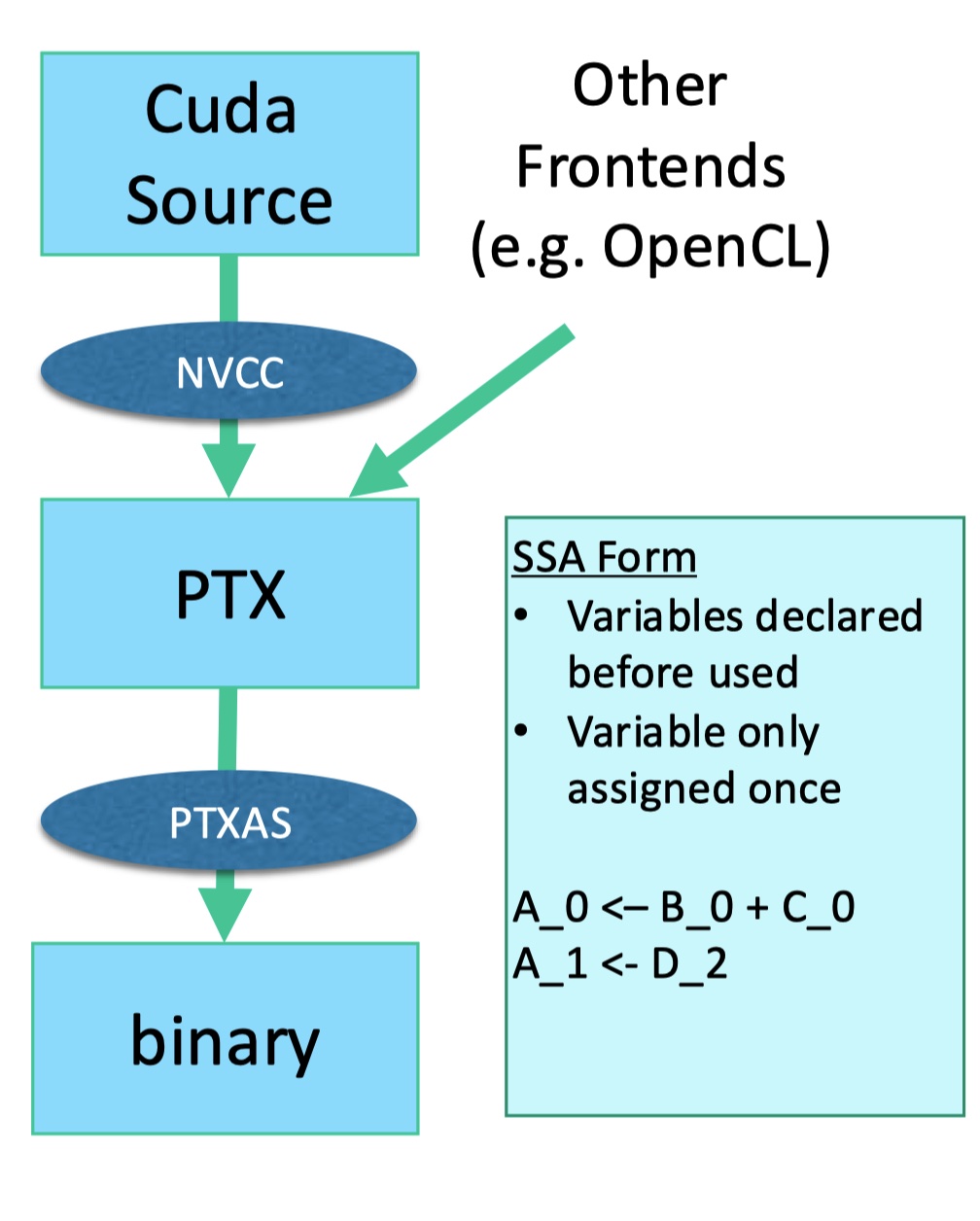
compile.jpg

CUDA源码会先经过nvcc编译成PTX，PTX时不依赖于特定GPU的，然后在用设备特定的 PTXAS backend compiler 将PTX做物理寄存器赋值。这样CUDA代码就拥有了可移植性，不再受特定设备型号限制。

PTX给所有的变量都赋予了虚拟寄存器，同时还做了predication支持，当遇到条件分支，会检测条件是否满足，若不满足，将会填充NOP。

Reference

https://docs.nvidia.com/cuda/archive/11.2.0/pdf/CUDA_C_Programming_Guide.pdf

Posted on Edited on In

CPU 缓存

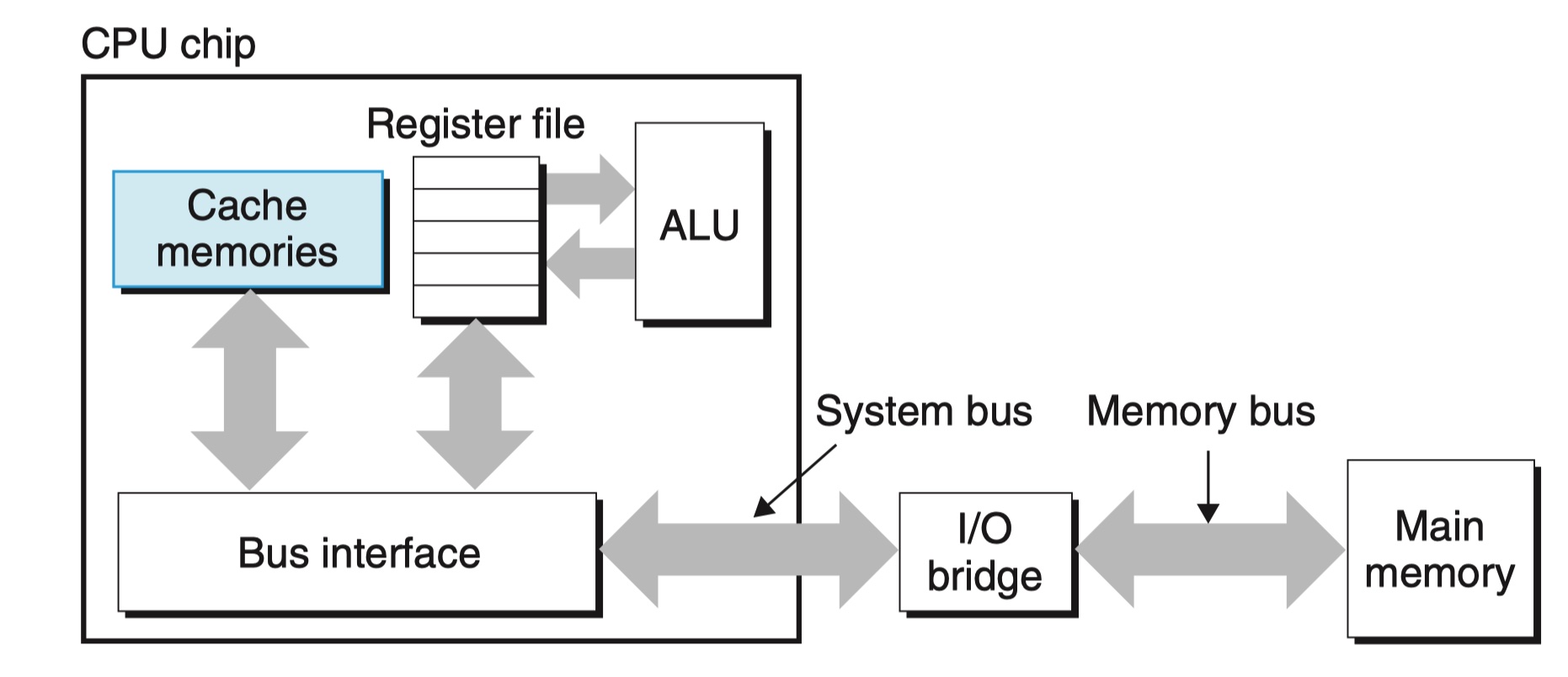
cache0.jpg

高速缓存包括：指令高速缓存 i-cache, 数据高速缓存 d-cache. 现代处理器用 i-cache 和 d-cache 替代了 unified-cache 从而方便并行读取一个指令字和一个数据字。

通用高速缓存存储器组织架构：

假设一个计算机的存储地址有 \(m\) 位，形成 \(M = 2^m\) 个不同的地址。这样一个机器的高速缓存被组织成一个有 \(S = 2^s\) 个高速缓存组，每个组包含 \(E\) 个高速缓存行，每个行由 \(B = 2^b\) 字节的数据块组成的存储空间。高速缓存组中的每一个高速缓存行由 \(1\) 位的 valid bit 声明是否含有有用信息，\(t\) 个不同 tag bit 用来标识每一个缓存行。

cache1.jpg

现代缓存地址会讲内存地址分解为标记位，块偏移位，和组索引位。

  • 组索引位用来找到数据所在的缓存组
  • 标记位告诉我们缓存组中的哪个缓存行包含了这个字，当且仅当valid位设为1，缓存行中才包含这个字
  • 块偏移位给出了该数据在缓存行中的偏移

cache2.jpg

从内存地址到缓存数据查找，本质上是将大的地址范围映射到小的地址范围，共有3种映射策略：

  1. 直接映射高速缓存：

    • 直接高速缓存就是每个缓存组中只有一个缓存行

    • 我们只需要通过组索引找到缓存组，看valid位是否置为1，再对比tag位，若匹配，则通过块偏移找到目标数据。

    • 缓存抖动

      1
      2
      3
      for (int i = 0; i < 8; i++) {
        sum += x[i] * y[i];  // 当 x[i]和 y[i]映射到相同的缓存组
      }

      这里因为缓存组里只有一个缓存行，高速缓存会反复加载和驱逐相同缓存组的缓存行

  2. 组相连高速缓存：

    • 映射过程就是上述通用高速缓存映射过程

    • 不命中替换：

      • 最近最少使用：Least-Recently-Used (LRU)
      • 最不常使用：Least-Frequently-Used (LFU)

      替换都需要额外的时间和硬件

  3. 全相连高速缓存：

    • 全相连高速缓存就是一个包含所有高速缓存行的高速缓存组
    • 映射时地址不划分组索引位，地址只被划分为一个tag和块偏移，从这一唯一的组中寻找数据与其他映射一致

局部性 (Locality):

  • 时间局部性 (Temporal): 最近使用的数据会再次使用
  • 空间局部性 (Spatial): 与过去使用过的数据内存相邻的数据会在不远的未来被使用

3种 Cache Misses:

  • Cold Miss: 当我们第一次使用这个数据
  • Capacity Miss: 缓存的空间不足
  • Conflict Miss: 缓存空间足够，但有太多的数据被映射到了相同的的缓存集，导致被替换

CPU指令流水线

这里我们通过 Loop Unroll 让

现代高性能CPU分支预测

分支预测发展历史：

Reference

CSAPP

https://blog.eastonman.com/blog/2023/12/modern-branch-prediction-from-academy-to-industry/

Posted on Edited on In

实验设备：AWS c7g.medium

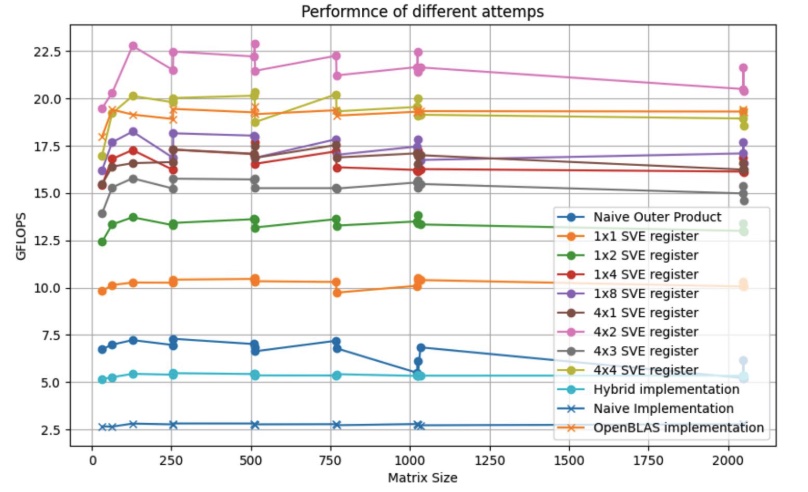
Result:

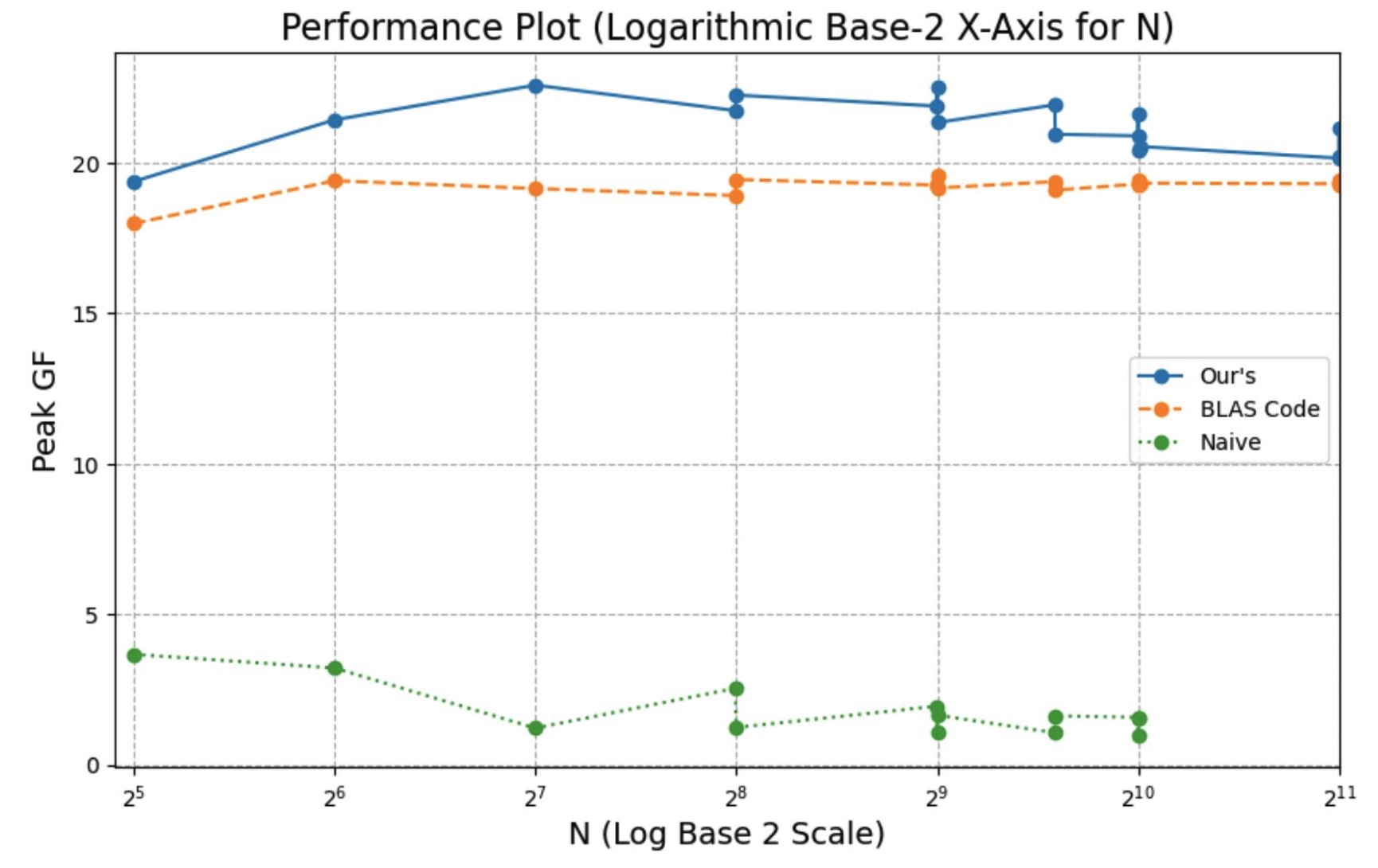
能跑赢 OpenBLAS (单核中)

pa1_result.jpg

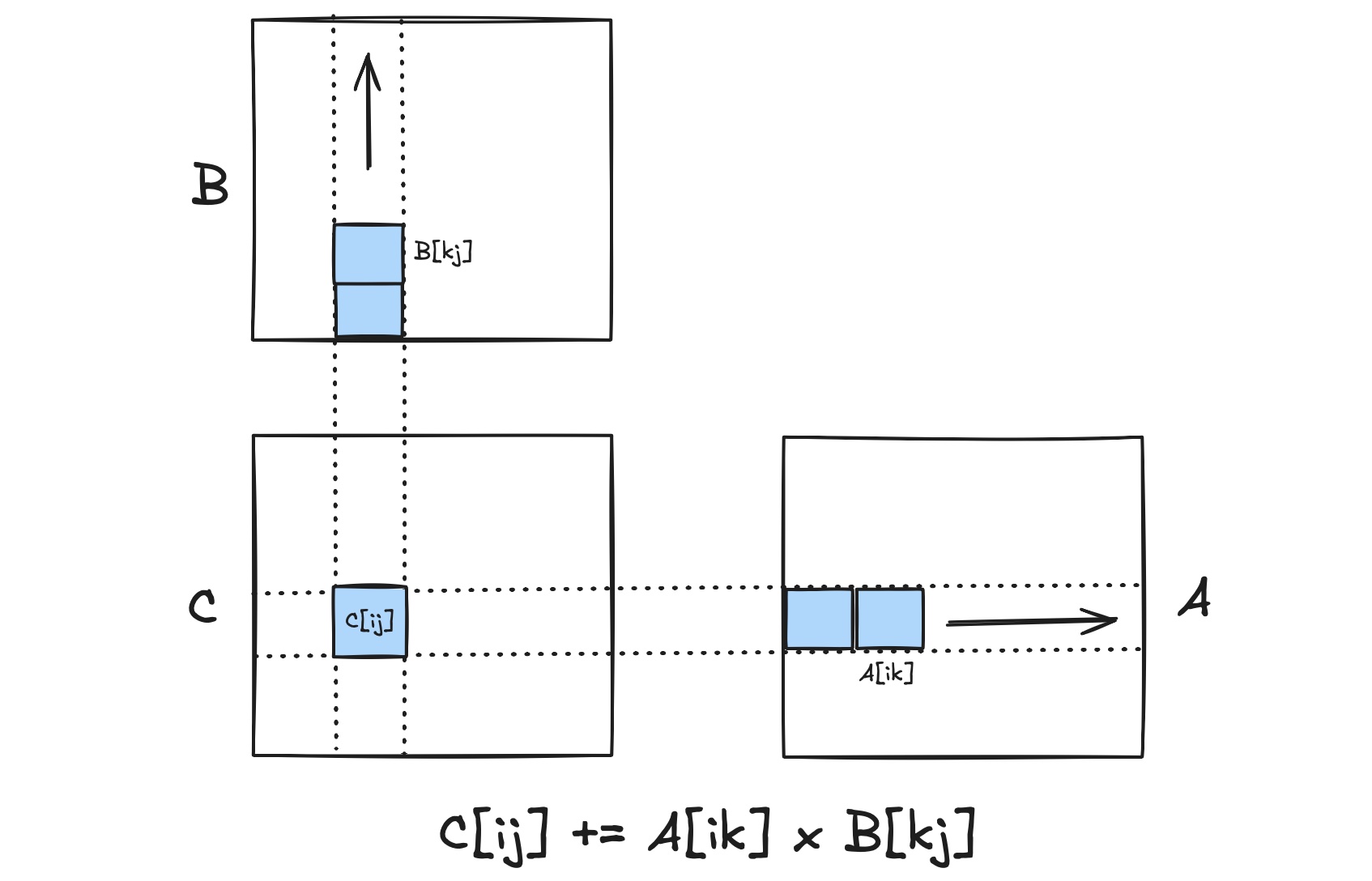
Naive GEMM

1
2
3
4
5
6
7
8
9
10
for (int i = 0; i < N; i++) {
  // 需要加载 n^2 / L 的A
  for (int j = 0; j < N; j++) {
      // 需要加载 n^3 的A
    	// 需要加载 n^2 / L 的C & 以及存储 n^2 / L 新的C
    for (int k = 0; k < N; k++) {
      C[i][j] += A[i][k] * B[k][j];
    }
  }
}

  • 总加载数：\(n^3 + 3n^2 / L\) (\(n\) 是矩阵的大小 \(L\) 是cache line大小)

  • 计算强度上限 : \[ q = \frac{2n^3}{n^3 + 3n^2 / L} < 2 \]

这里我们的 \(q\) 被制约，导致程序性能落入了 bandwidth bound，即由于程序的内存利用率低下，带宽制约了程序的性能提升。解决方案有两个：升级硬件并提升带宽，增加计算强度上限 (\(q\))

从运行时间预测公式也可以得出相同结论： \[ predicted \ time = ft_f (1 + \frac{t_m}{t_f}\times \frac{1}{q}) \]

  • \(t_m\) 是传递一个单位的数据耗时
  • \(t_f\) 是一个计算操作的耗时
  • \(f\) 是计算操作的数量
  • \(ft_f\) 是性能峰值

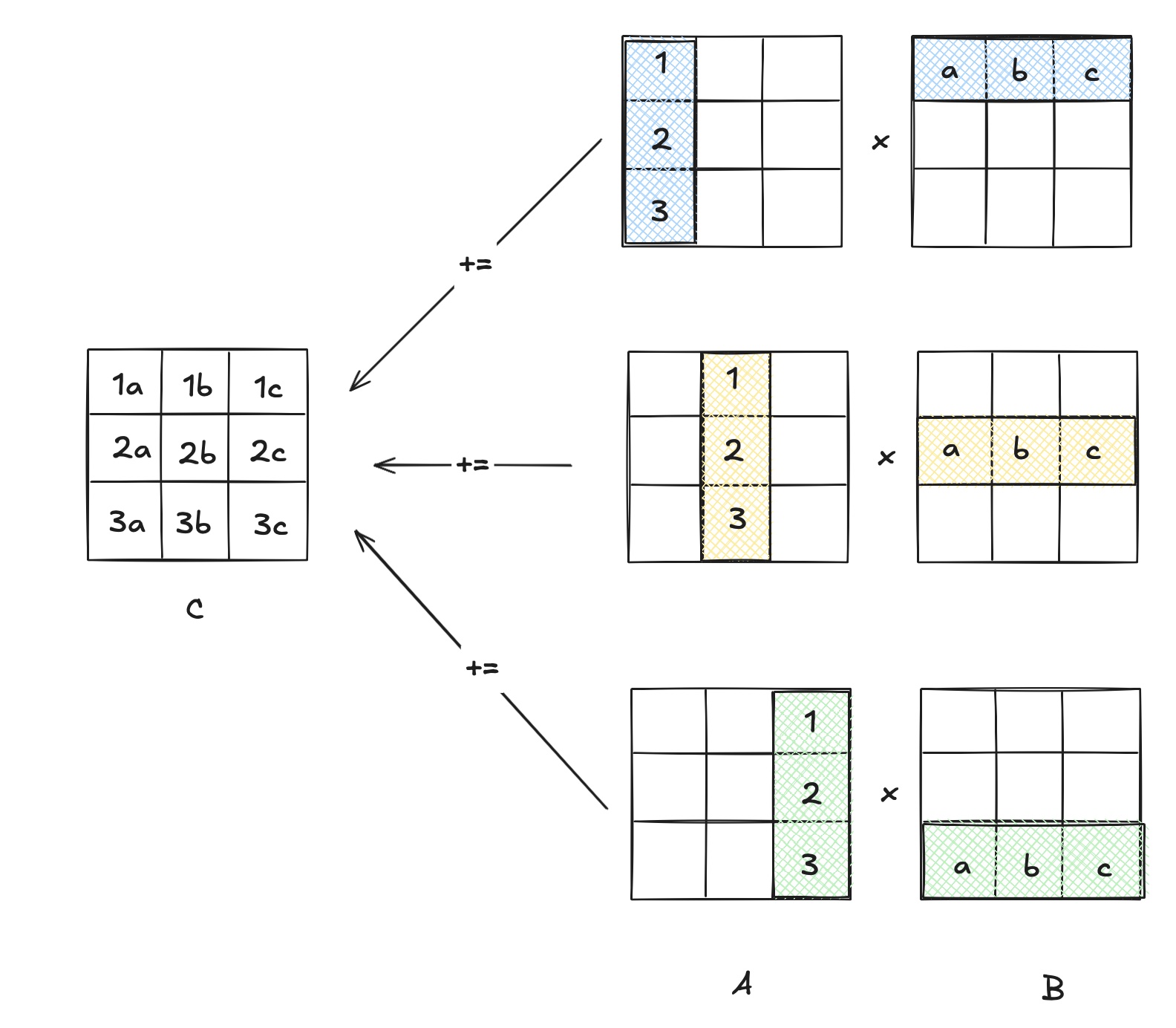
Blocked GEMM

  • Blocked GEMM - 内积

    blockedGEMM.jpg

    1
    2
    3
    4
    5
    6
    7
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
        for (int k = 0; k < N; k++) {
          C[i,j] += A[i,k] * B[k,j];  // 计算C[ij]这个块
        }
      }
    }
    • 每行 & 列被分为 \(N\) 个块
    • 加载 C： \(\frac{N^2 \times (n / N)^2}{L}= \frac{n^2}{L}\)
    • 加载 A & B： \(\frac{2 \times N^2 \times N \times (n / N)^2}{L}= \frac{2n^2N}{L}\)
    • 存储 C: \(\frac{N^2 \times (n / N)^2}{L}= \frac{n^2}{L}\)

    \[ q = \frac{2n^3}{(2N + 2)n^2/L} \propto \frac{n}{N} \]

  • Blocked GEMM - 外积

    BlockedGEMM1.jpg

    1
    2
    3
    4
    5
    6
    7
    for (int k = 0; k < N; k++) {
    	for (int i = 0; i < N; i++) {
      	for (int j = 0; j < N; j++) {
          C[i,j] += A[i,k] * B[k,j]; // 计算C[ij]这个块
        }
      }
    }
    • 每行 & 列被分为 \(N\) 个块
    • 加载C：\(\frac{N\times n^2}{L}\)
    • 加载A：\(\frac{n^2}{L}\)
    • 加载B：\(\frac{N\times n^2}{L}\)
    • 存储C：\(\frac{N\times n^2}{L}\)

    \[ q = \frac{2n^3}{(3N + 1)n^2/L} \propto \frac{n}{N} \]

数据传输 Naive vs Outer vs Inner product (非方阵情况 m, n, k):

对 m 分了 M 块，对 n 分了 N 块，对 k 分了 K 块

Matrix Naive Product Inner Product Outer Product
C \(2mn / L\) \(2mn / L\) \(2Kmn / L\)
A \(mk / L\) \(Nmk / L\) \(mk / L\)
B \(mkn / L\) \(Mnk/L\) \(Mnk / L\)

在三种实现的数据传输中，内积和外积在传输操作数上对naive实现有数量级上的优势。对比inner product 和 outer product, 不难发现inner product 在传输 C 所用的操作较少，传输 A 时用的操作较多。我们可以根据实际矩阵乘法的 C 和 A 的大小来决定使用inner product 还是 Outer product。

性能分析：

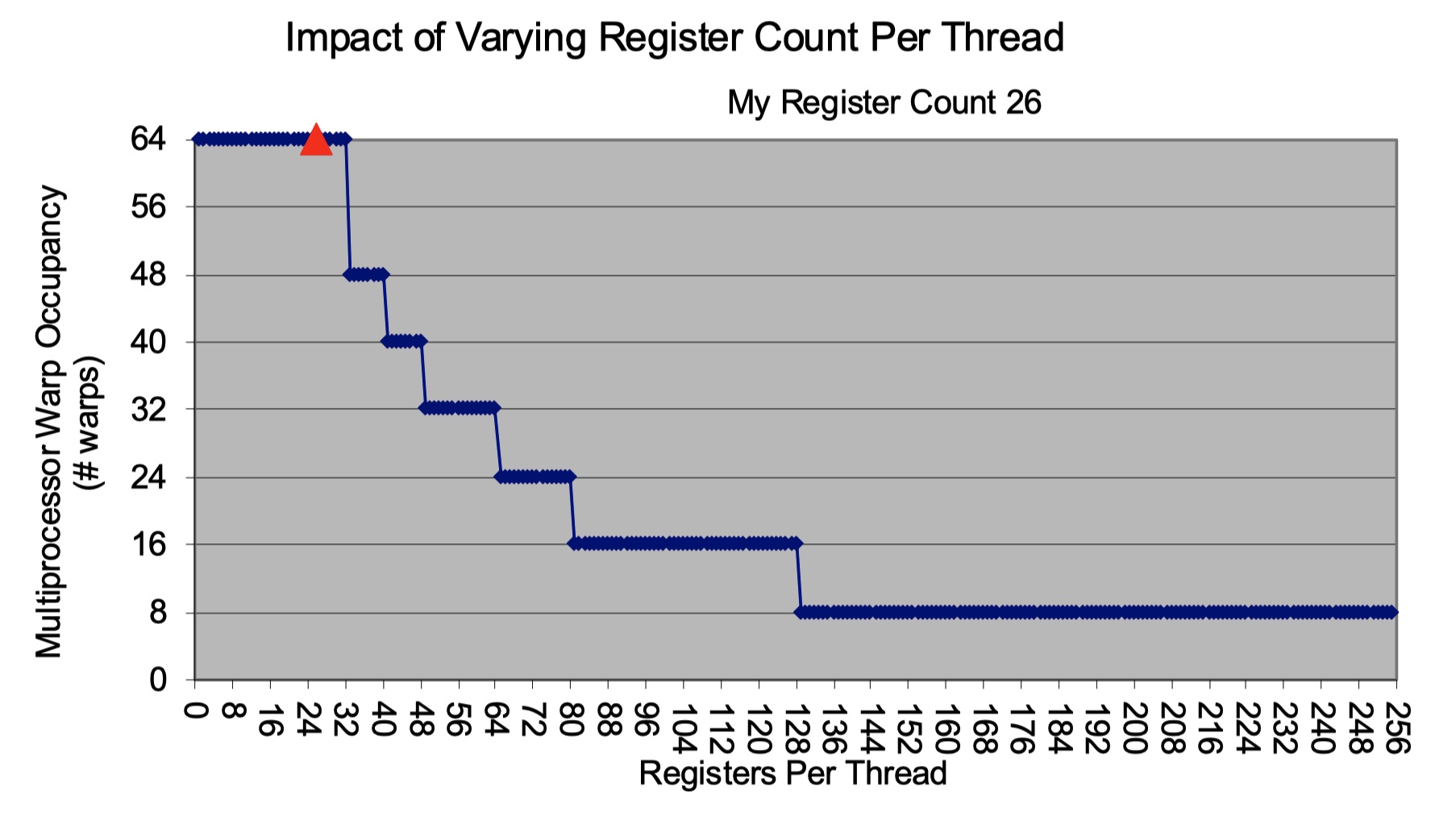
我们希望 \(q\) 尽可能大，根据公式，我们无法调节问题规模 \(n\), 只能尽量调小 \(N\), 即把子矩阵分割的更大，让块的数量更小。然而在实际实现中，我们还需要考虑缓存的大小。如果将子矩阵分割太大导致其无法被装进缓存里，这将大大降低其性能。因此我们应尽量让找到一个子矩阵大小的临界值并将其设为N。

假设 \(M_{fast}\) 是快速存储空间 (\(L1\) 或 \(L1 + L2\))，我们希望将 \(A\), \(B\), 和 \(C\) 放入 \(M_{fast}\) 中。因此 \(N\) 必须大于 \(n \times (3/M_{fast})^{\frac{1}{2}}\)。因为我们想要 \(N\) 越小越好，从而最大化 \(q\)。因此，如果我们能正确使用 \(M_{fast}\): \[ q = \frac{2n^3}{(2(n(\frac{3}{M_{fast}})^{\frac{1}{2}}) + 2) \times n^2/L} \approx L\times (M_{fast} / 3)^{1/2} \] 这是通过内积公式推导的，外积公式只有常量改变，推导出的 \(q\) 性能公式与内积推导出的相同。从这个公式我们发现 \(q\) 只与 \(M_{fast}\) 有关。回忆 predicted time 的计算公式 \[ predict \ time = ft_{f} (1 + (\frac{1}{\frac{t_f}{t_m}})(\frac{1}{q})) \] 我们可以计算出想要达到理论性能峰值的百分比至少需要多大的缓存 (lower bound)。假设我们想要达到理论性能峰值的50%： \[ predicted \ time = ft_f \times 2 \\ that \ is: \ \ \ (\frac{1}{\frac{t_f}{t_m}})(\frac{1}{q}) = 1 \\ then: \ \ \ \ \ q = \frac{t_m}{t_f} \\ \text{We know:} \ \ \ q \approx L(M_{fast} / 3)^{1/2} \\ M_{fast} = 3 \times (t_m / (Lt_f))^2 \] 至此我们算出加入我们想让性能达到理论峰值的50%，我们至少要让 \(M_{fast}\) 达到这个数值。注意：这个公式只表示理论下限，实际上 \(M_{fast}\) 应该要更大些。

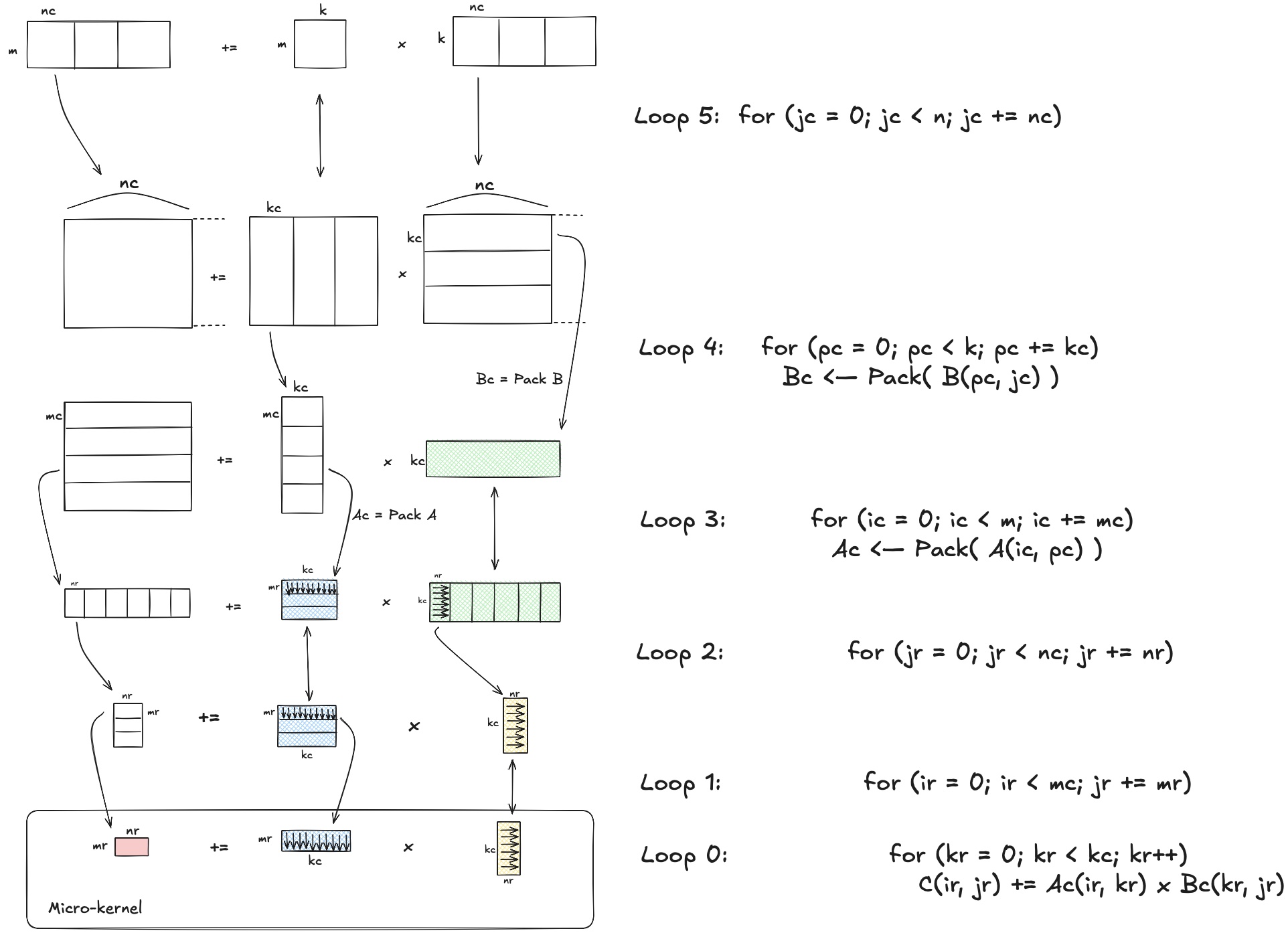
最大限度使用分层缓存：BLIS框架

blislab.jpg

BLIS框架的主要特点是优化矩阵乘法的计算过程，使计算能最大化利用CPU的多级缓存（L1、L2、L3）。特别是BLIS框架通过将复杂计算分解为一个需要高度优化的小型内核（micro-kernel），显著降低了需要直接优化的代码量。

这里BLIS框架把数据分成了多个块，在块中的数据也被划分到了更小的块。这样的划分可以让程序：

  • 将小块数据存储在L1缓存中，供微内核重复使用。
  • 将矩阵更大块存储在L2缓存中，可以通过分块降低数据传输的延迟。
  • 将大块数据驻留在其L3，供多个L2块复用。

在上述程序中，A的块 \((mr, kc)\) 被保存在 L2 缓存中，降低访问延迟。B的块 \((kc, nr)\) 被保存在 L1 缓存中，他将被 A 的块重复使用。

注意：我们无法显式的将某段数据存放在某一个缓存层中，数据被放置在哪由它的出现频率决定 (缓存调度规则也有影响)。我们说 B 的块被缓存在 L1 中是因为 B 块中相同数据出现频率比较高。根据缓存调度规则，我们认为这部分数据会被”尽可能地“存储在L1中。

分块的本质是为了给用户提供可调节的参数，让应该在L1中的数据不出现在L2，应该出现在 L2 的数据不出现在 L3。

我们在做分块的时候还可以根据情况做 Packing，packing 将 \(A\) 和 \(B\) 中需要连续访问的数据重新排序使之存放在连续的内存空间中。这样做 CPU 在访问内存时，可以高效使用cacheLine，同时 cache 内存储的都是需要被使用的数据，将conflict miss降到最低。

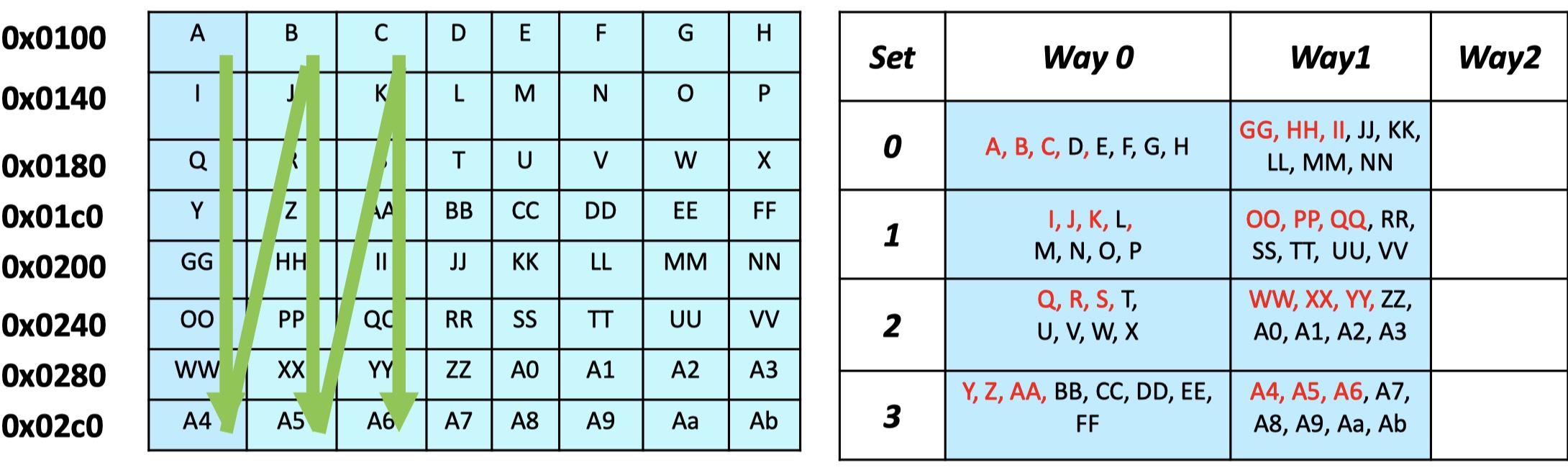
packing.jpg

这里是一个没有packing过的数据，缓存行大小 = 64 bytes，8 bytes / element。我们可以算出一个缓存行会抓取 8 个element。因此右图是数据在缓存中的存储方式。我们可以发现在一个缓存块中我们当前需要的元素只占一小部分。这会导致缓存利用率较低。即便我们可能会在后续使用 "D E F G H ...", 我们无法保证这个缓存块不会被替换因为 way 也是有限的，也就是会发生 conflict miss。

提升Micro-Kernel性能：SIMD

SIMD 是CPU层面的加速，有特定硬件支持。

1
2
MMX, SSE[1:5], AVX: x86
NEON, SVE: ARM

以SVE为例，支持SVE得架构提供了32个可伸缩向量寄存器，16个可伸缩的Predicate寄存器等等。

  • 可伸缩向量寄存器：可存储一个向量的数据 (支持64, 32, 16, 8位 & 单精度 & 双精度)
  • 可伸缩 Predicate 寄存器： 控制哪些元素参与计算

\[ \mathbf{C} = \begin{bmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \cdot \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} \]

用SIMD实现： \[ <c_{11}, c_{21}> \text{+=} <a_{11}, a_{11}> · <b_{11}, b_{12}> \] \[ <c_{11}, c_{21}> \text{+=} <a_{12}, a_{12}> · <b_{21}, b_{22}> \] \[ <c_{12}, c_{22}> \text{+=} <a_{11}, a_{21}> · <b_{12}, b_{12}> \] \[ <c_{12}, c_{22}> \text{+=} <a_{12}, a_{22}> · <b_{22}, b_{22}>\\ \]

1
2
3
4
5
6
7
register svfloat64_t a; // if vlen = 256b, 这可以存放4个double
veca = svldl(pred, A + i);  // 将内存中 A + i 加载到veca
svst1_f64(pred, C+i, vecc);  // 将vecc的数存储到内存中
svwhilelt_b64(i, N);  // 返回一个谓词寄存器，每一位表示对应索引状态 - true：索引<n, otherwise false
svptest_any(svptrue_b64(), pred);  // 检测谓词寄存器中是否至少有一个true
svdup_f64(aval); // 返回一个向量，里面全部填充aval
svmla_f64_m(npred, c0x, bx, ax);  // c0x += bx * ax （npred控制哪些位生效，哪些不生效）

向量和predicate的组织结构：

predicate.jpg

访存优化:

Alignment (数据对齐)

数据对齐的要求是不同对象在内存中存放的位置为 \(2^n\) 的倍数 (\(n\) 根据数据类型而不同，Linux 对short类型要求是2的倍数，对int, double这种要求是4的倍数)。数据对齐的意义：一个处理器通常能从内存读取一个缓存行的数据。如果数据未对齐，可能会跨越两个缓存行 (Cache Line Crossing), 导致性能损失。同时，如果数据访问跨越内存页面边界，可能需要额外的地址转换操作 (TLB Miss)。

1
_aligned_malloc; // 可以指定对其边界分配内存

Handling of Stores (存储操作处理)

  • 流式存储指令 (Streaming Store Intructions)

    存储时直接写回到内存，不会分配到缓存，适用于不太可能被重用/无法装入缓存的数据，同时避免了缓存污染

    1
    sve_stnt1_f64;

  • 写合并 (Write Combining)

    如果硬件支持写合并，会有一个写合并缓冲区 (Write Combining Region)，存储小的写入合并，并将他们合并成一个较大的事务。注意：写合并以来连续内存区域，因此数据必须对齐。写合并最适用于流式访存。

提高指令并行度: Loop Unroll

Loop Unroll 让在一个循环中让更多的寄存器被使用。在unroll后，可以让计算和加载交替进行，增加了指令并行性 (指令流水线)，促进CPU进行指令流水线优化。由于向量寄存器存在上限，如果使用寄存器超过上限便要进行压栈操作，从而降低性能。

pa1_result2.jpg

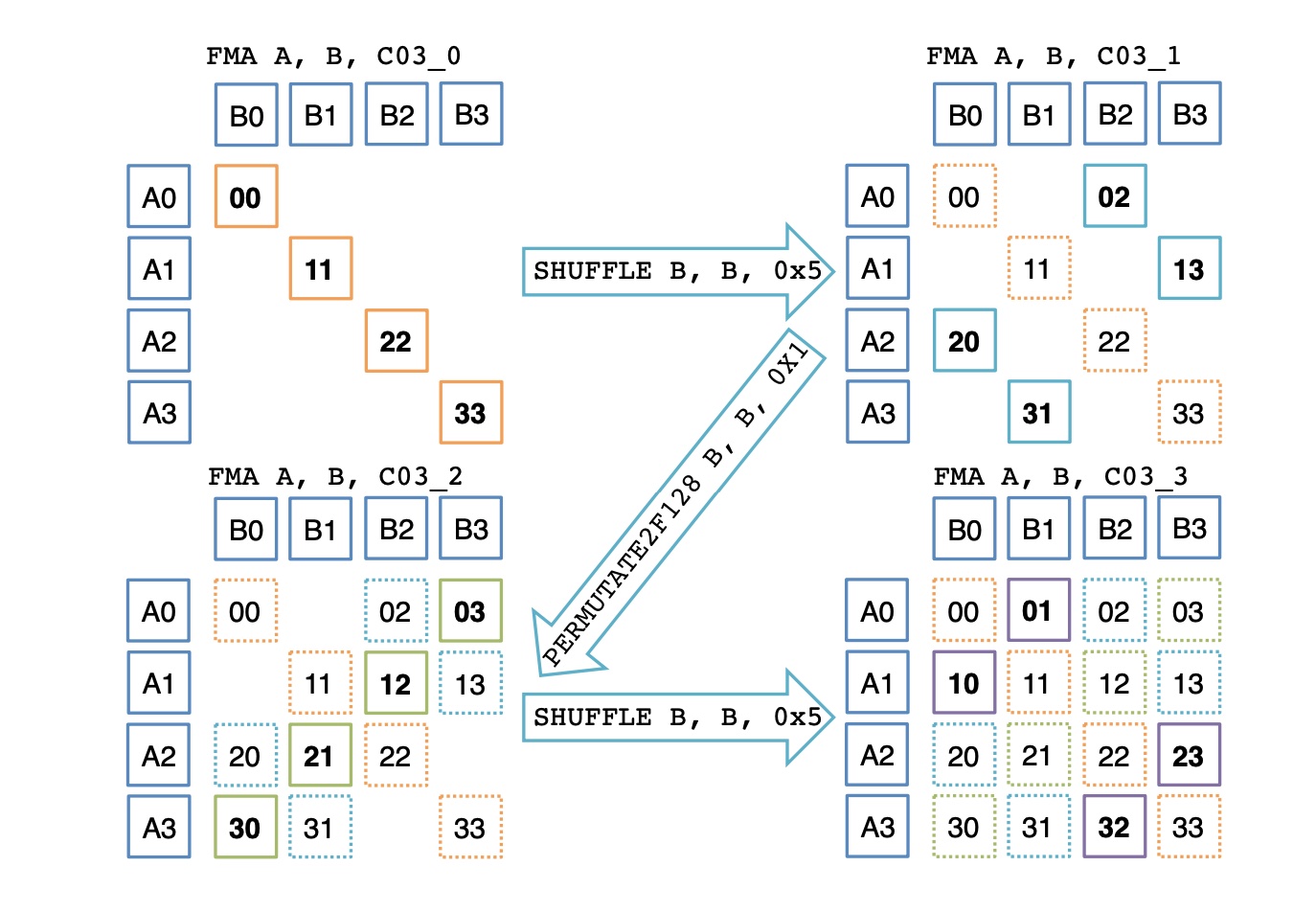
附: Butterfly Method - 理论王者

理论上butterfly Method 避免了广播，操作更少，小于应该更高。但我们目前实现的效果并不好.

butterfly.jpg

  • 初始值：[\(A_0\), \(A_1\), \(A_2\), \(A_3\)], [\(B_0\), \(B_1\), \(B_2\), \(B_3\)]
  • 对 \(B\) 交换前半部分和后半部分：[\(A_0\), \(A_1\), \(A_2\), \(A_3\)], [\(B_2\), \(B_3\), \(B_0\), \(B_1\)]
  • 对 \(B\) 前半部分和后半部分分别内部交换：[\(A_0\), \(A_1\), \(A_2\), \(A_3\)], [\(B_3\), \(B_2\), \(B_1\), \(B_0\)]
  • 对 \(B\) 交换前半部分和后半部分：[\(A_0\), \(A_1\), \(A_2\), \(A_3\)], [\(B_1\), \(B_0\), \(B_3\), \(B_2\)]

此时 \(C\) 的所有结果都已经算出来了，但是乱序的 (如图)。

重新排序 （12 instructions）：

butterfly2.jpg

Reference

https://arxiv.org/pdf/1609.00076